2025-12-29

从OSS叛逃到安全炼狱：我的全栈开源硬核之路

凌晨1点的账单惊吓

“一个月300块？就存点头像图片？”

我盯着阿里云OSS的测试账单，手抖得比咖啡因过量还厉害。这还只是测试期的费用，真上线了还得了？

“不行，”我咬牙，“这违背开源精神。”

作为一个开源项目的维护者，我有个固执的原则：绝不让用户为开源项目花一分钱。OSS？拜拜了您嘞。

一周内的技术栈大迁移

周一，我做出了那个改变一切的决定：从OSS迁移到本地存储。

“简单，”我想，“Docker + Nginx，文件存本地，零成本。”

周二，我开始改造。后端Java代码好办，但前端上传怎么办？我瞄了一眼Vue组件——一个头像上传组件就400多行代码，各种校验、预览、裁剪。

“让trae帮我弄吧。”我偷了个懒。

trae的天真设计

我对IDE里的trae说：“帮我改一下头像上传，不用OSS了，存本地Nginx。”

trae秒回方案：“收到。使用Vite反向代理，前端直接上传到/uploads目录，Nginx直接服务。”

代码很简单：

javascript
// 上传
POST /uploads 
// 前端直接处理，不走Java

我测试了一下，速度飞快。Node.js处理文件上传，确实比Java省资源。

但周三，我发现一个问题：用户上传新头像，旧头像还在服务器上躺着！

“这不行，”我的资源洁癖发作了，“如果有人恶意上传，服务器不就炸了？”

我命令trae：“加删除逻辑。用户上传新头像前，先删除旧头像。”

trae很听话，把单次上传改成了两个操作：

删除旧头像（DELETE /uploads/旧文件）
上传新头像（POST /uploads）

“完美。”我当时想。

周四的噩梦降临

周四晚上，预上线前的最后一次安全测试。

我随手在APIFox里试了一下：


DELETE http://test.zymusic.top/uploads/admin.png

200 OK。

我又试了试：


POST http://test.zymusic.top/uploads
（随便传个文件）

200 OK。

我的血液凝固了。

这两个接口完全没有权限验证！任何人，不需要登录，就能删文件、传文件！

“我草！trae你……”我骂到一半，突然意识到：trae只是个AI，它懂个屁的权限验证。

问题的核心矛盾

凌晨2点，我盯着架构图，发现了几个致命矛盾：

矛盾一：性能 vs 安全

Node.js处理文件IO性能好，但不会解析JWT（Java生成的）
Java会解析JWT，但处理文件IO性能差
我既想要Node.js的性能，又想要Java的安全

矛盾二：资源洁癖 vs 安全风险

不删旧文件 → 服务器可能被恶意上传撑爆
删旧文件 → 权限漏洞可能被黑客利用
我的资源洁癖逼我选择了更危险的路

矛盾三：开源理想 vs 工程现实

理想：完全免费，不依赖任何付费服务
现实：安全方案要么花钱（OSS），要么花精力（自研）
我选择了最硬核也最危险的路

周五凌晨的绝地求生

凌晨3点，我必须在几个小时内解决这个问题，否则周一预上线就是个笑话。

方案一：让前端直接问Java权限（不行） 因为最终文件操作还是要和Nginx交互，JavaScript处理IO比Java高效得多。而且，让JS解析JWT？不可接受！JWT是Java生成的，就该Java来解析。

方案二：让Java直接管理文件（不行） 性能下降不说，还要大改前后端，一周时间根本不够。

方案三：在Node.js和Nginx之间加一层验证（可行！）

我的方案渐渐清晰：

前端调用Node.js的上传/删除接口
Node.js先向Java后端请求授权
Java验证JWT，返回是否允许操作
Node.js根据授权结果执行文件操作

用Redis搭建“操作锁”

但还有个问题：如何确保用户是“先删后传”，而不是只传不删，或者只删不传？

我的解决方案：用Redis记录操作状态。

javascript
// Node.js上传服务伪代码

// 删除接口
app.delete('/uploads/:filename', async (req, res) => {
  // 1. 从header拿到JWT
  const token = req.headers.authorization;
  
  // 2. 问Java：这人有权限删这个文件吗？
  const canDelete = await javaBackend.verifyDelete(token, filename);
  
  if (!canDelete) {
    return res.status(403).send('滚犊子');
  }
  
  // 3. 执行删除
  await fs.unlink(filepath);
  
  // 4. 在Redis标记：这个用户已删除旧头像，可以上传新的了
  await redis.setex(`upload_ok:${userId}`, 5, '1');
  
  res.send('删除成功');
});

// 上传接口
app.post('/uploads', async (req, res) => {
  const token = req.headers.authorization;
  
  // 1. 问Java：这人有权限上传吗？
  const canUpload = await javaBackend.verifyUpload(token);
  
  if (!canUpload) {
    return res.status(403).send('没权限');
  }
  
  // 2. 检查Redis：他是不是刚删了旧头像？
  const canProceed = await redis.get(`upload_ok:${userId}`);
  
  if (!canProceed) {
    return res.status(403).send('请先删除旧头像');
  }
  
  // 3. 执行上传
  const newFilename = await saveFile(req.file);
  
  // 4. 清理Redis标记
  await redis.del(`upload_ok:${userId}`);
  
  res.send({filename: newFilename});
});

Java后端的验证逻辑：

java
// Java伪代码
public boolean verifyDelete(String token, String filename) {
  // 1. 解析JWT，获取用户ID
  String userId = decodeJWT(token);
  
  // 2. 查数据库，这个用户的当前头像是不是这个文件？
  User user = userDao.findById(userId);
  if (user.getAvatar().equals(filename)) {
    return true; // 是自己的头像，可以删
  }
  
  return false; // 不是自己的头像，滚
}

public boolean verifyUpload(String token) {
  // 管理员？直接放行！
  if (isAdmin(token)) {
    return true;
  }
  
  // 普通用户：检查是否有上传权限（比如是不是被封禁了）
  return userCanUpload(token);
}

周六凌晨的缝合怪架构

凌晨4点，我部署完这个“四不像”的架构：

前端 → Node.js上传服务 → Java权限验证 → Redis状态管理 → Nginx文件服务

绕了地球一圈，但：

安全了（所有操作经过Java验证）
性能保留了（Node.js处理文件IO）
资源洁癖满足了（旧文件会被删除）
开源精神坚持了（没花一分钱）

“这就是工程现实吗？”我苦笑，“为了不花钱，我造了个比OSS复杂十倍的轮子。”

周日的最后反思

系统终于安全了。我瘫在椅子上，回顾这一周的过山车：

1. 开源不等于免费

我以为“不花钱”就是开源精神，但忽略了“不花钱”可能意味着“花更多精力”。OSS的300块，买的是别人解决好的安全方案。我省了300块，搭进去一周的睡眠。

2. 资源洁癖是种病，但得治

我的担心是对的——恶意上传真的能搞垮服务器。但我的解决方案错了——不应该为了省资源而牺牲安全。应该先保证安全，再考虑资源。

3. AI是工具，不是工程师

trae能写出漂亮的代码，但不懂架构、不懂安全、不懂权衡。它能执行命令，但不能思考后果。把AI当工程师用，就像让厨子开飞机——早晚出事。

4. 性能与安全的永恒战争

我既想要Node.js的IO性能，又想要Java的安全验证。鱼和熊掌不可兼得，但我用Redis和HTTP调用强行兼得了。代价是：复杂度爆炸。

5. 一周能改变什么？

一周前，我以为只是换个存储方案。一周后，我造了个分布式文件权限系统。有时候，工程进度不是按计划走的，是按问题走的。

给所有开源硬核玩家的忠告

如果你也在维护开源项目，想坚持“完全免费”，记住我的教训：

1. 安全永远第一

用户能接受功能少，但不能接受数据丢。安全漏洞是开源项目的死刑。

2. 复杂度是隐形成本

你省了云服务的钱，但付出了开发、维护、调试的精力。这些精力也是成本。

3. 测试，测试，再测试

特别是安全测试。我要是早做安全测试，周二就能发现问题，不用拖到周四凌晨。

4. 承认工具的限制

AI能帮你写代码，但不能帮你做架构决策。你是工程师，它是工具。别搞反了。

5. 有时候，花钱买时间是对的

300块买OSS服务，还是300小时造轮子？在开源项目里，时间也是稀缺资源。

最后

窗外天空泛白，一周的挣扎结束了。

我的开源项目依然坚持“完全免费”，但代价是：一个比商业方案复杂十倍的权限系统。

这值得吗？我不知道。

但我知道的是：当用户不用为这个项目花一分钱时，他们不会知道，有个傻子在深夜用Redis、Node.js、Java和Nginx，造了个丑陋但安全的轮子。

而那个傻子，现在需要睡一觉。

预上线倒计时：12小时。

这次，真的准备好了。🚀

2025-12-10

1581. 进店却未进行过交易的顾客

https://leetcode.cn/problems/customer-who-visited-but-did-not-make-any-transactions/description/?envType=study-plan-v2&envId=sql-free-50

sql
# Write your MySQL query statement below
select vis.customer_id,sum(if((tra.transaction_id is null), 1,0)) count_no_trans 
from visits vis
left join Transactions tra 
on vis.visit_id=tra.visit_id
group by vis.customer_id
having count_no_trans >0;

197. 上升的温度

https://leetcode.cn/problems/rising-temperature/description/?envType=study-plan-v2&envId=sql-free-50

sql
# Write your MySQL query statement below
select w2.id
from Weather w2
join Weather w1
on datediff(w2.recordDate,w1.recordDate)=1 
where w2.Temperature > w1.Temperature;

2025-12-06

全局锁

锁的是整个数据库实例，也就是数据库中的所有表，加了全局锁之后，所有客户端只能进行读操作，不能其他操作。

用途：用于备份数据库，防止备份途中有修改操作导致数据不一致

加全局锁

sql
flush tables with read lock;

备份

sql
mysqldump -uroot –p1234 itcast > itcast.sql

释放锁

sql
unlock tables;

特点：在加了全局锁之后，只能读，会导致需要修改的业务处于阻塞状态

在InnoDB引擎中，我们可以在备份时加上参数--single-transaction参数来完成不加锁的一致性数据备份。

sql
mysqldump --single-transaction -uroot –p123456 itcast > itcast.sql

表级锁

表锁

分为两类：表共享读锁（read lock），表独占写锁（write lock）。

读锁：所有客户端只能读，包括自己。

写锁：其他客户端既不能读，也不能写；自己既可以读也可以写。

语法：

加锁：

sql
lock tables 表名 read/write;

释放锁：

sql
unlock tables;（或者直接停止客户端连接）

2025-12-01

A

由于序列单调不降，所以只要体力足够往下一列走就往走向下一列；否则，一直沿着当前列走直到体力不小于下一列所需的值。假设当前列还差体力值 $x$ 才能走到下一列，当前列的权值为 $y$ ，那么需要继续在当前列走 $\lceil x/y \rceil$ 次。 $\lceil x \rceil$ 表示对 $x$ 表示向上取整，模拟这个过程，直到走到第 $n$ 列时直接跳到最后一行，或者走到最后一行时停止即可。

时间复杂度为 $O(n)$ 。

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int M = 1e6 + 10;
#define endl '\n'
int a[M], b[M], c[M];
void solve()
{
    int k, n;
    cin >> k >> n;
    vector<int> a(n + 2);
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    int ans = a[1], x = 1, y = 1;//x，y分别表示当前所在行和列
    while (1)
    {
        // cout << x << ' ' << y << ' ' << ans << endl;
        if (x == k)//到达最后一行了直接退出
            break;
        if (y == n)//到达最后一列了，直接跳到最后一行
        {
            ans += (k - x) * a[n];
            break;
        }
        if (a[y + 1] - ans > 0)//不能直接走到下一列，只能先在当前列走
        {
            int t = min(k - x, (a[y + 1] - ans + a[y] - 1) / a[y]);//这里是在做向上取整
            ans += t * a[y];
            x += t;
            if (x == k)
                break;
            x++;
            y++;
            ans += a[y];
        }
        else//可以直接走到下一列
        {
            y++;
            x++;
            ans += a[y];
        }
    }
    cout << ans  << endl;
}
signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)
        solve();
}

B

由于每个数最多只有 $6$ 位，直接枚举交换哪两位复杂度是可以接受的，暴力即可。

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int M = 1e6 + 5;
const int mod = 1e9 + 7;
int a[M];
void solve()
{
    int n;
    cin >> n;
    int sum = 0;
    for (int i = 1; i <= n; i++)
    {
        string s;
        cin >> s;
        string ans = s;
        int l = s.size();
        for (int i = 0; i < l; i++)
        {
            for (int j = i + 1; j < l; j++)
            {
                string t = s;
                swap(t[i], t[j]);
                ans = max(ans, t);
            }
        }
        sum += stoi(ans);//把字符串转换为整数的函数
    }
    cout << sum << endl;
}
signed main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    cin >> T;
    while (T--)
    {
        solve();
    }
}

C

题意没有弯弯绕绕，就是表面意思。对于 $i$ ，单独计算左右的贡献然后加起来即可。现在考虑左边的贡献应该如何计算，我们从 $i$ 出发，往左遍历，遇到不小于当前最大值的数字就把他加入，并将他更新为当前的最大值。

这样的策略是正确的，因为假设我们选择了一个下标 $j(1 \le j \le i)$ ， $a_j$ 是区间 $[i,j]$ 的最大值，那么对于该区间内的所有能选择的数，我们一定可以通过刚才描述的策略把他们选到，如果你遇到能选择的数却最不选择，得到的结果不会更优。（自己随便举几个例子）

现在的瓶颈在于原来的模拟是每一次 $O(n)$ 的，我们如果模拟 $n$ 次是不行的，我们需要快速计算当前字数左边中，离他最近且不低于他的数字所在的位置，这个是单调栈的模板，然后只需要做一次递推即可求解。右边的贡献计算同理。单调栈学习链接：https://www.luogu.com.cn/problem/P5788

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define endl '\n'
const int N = 1e6 + 5;
const int mod = 1e9 + 7;
int a[N];
pii b[N];
void solve()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    vector<int> l(n + 2), r(n + 2);
    stack<pair<int, int>> p;
    // 左边最近的大于等于a[i]的下标
    for (int i = n; i >= 1; i--)
    {
        while (!p.empty() && a[i] >= p.top().first)
        {
            l[p.top().second] = i;
            p.pop();
        }
        p.push({a[i], i});
    }
    while (!p.empty())
        p.pop();
    // 右边最近的大于等于a[i]的下标
    for (int i = 1; i <= n; i++)
    {
        while (!p.empty() && a[i] >= p.top().first)
        {
            r[p.top().second] = i;
            p.pop();
        }
        p.push({a[i], i});
    }
    for (int i = n; i >= 1; --i)
        r[i] = r[r[i]] + 1;
    for (int i = 1; i <= n; ++i)
        l[i] = l[l[i]] + 1;
    for (int i = 1; i <= n; i++)
        cout << l[i] + r[i] - 1 << " ";
    cout << endl;
}
signed main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    cin >> T;
    while (T--)
    {
        solve();
    }
}

D

太难，略

E

首先把出现次数小于 $x$ 的数所在位置隔开，这些数字所在的区间一定不满足条件，于是原序列被划分成了若干个子段，每一段可以分开单独计算。

每个段中的数字，在整个数组出现的次数都不小于 $x$ ，而 $\sqrt{n} \leq x$ ，所以剩余的数的种类不会超过 $\sqrt{n}$ 种。

考虑模拟暴力过程，从当前端点开始，往后跳跃到当前数字后面第 $x$ 次出现的位置，如果发现跳跃的这一段位置中有新数字被加入，则对右端点取最大值并继续执行上述过程；否则直接停止，当前右端点就是满足条件的最小右端点。

如果新加入的数字后面已经不足 $x$ 个，直接判为 $-1$ 。

例如， $n=4,x=2$ ，序列为 $\{1,2,1,2,\}$ ，假设左端点为 $1$ ，右端点从 $1$ 更新为 $3$ ，此时发现新数字 $2$ 被加入，于是继续跳跃扩展右端点到 $4$ 。

而我们在跳跃过程中只关注每种数第一次出现的位置，然后进行跳跃，可以倒序枚举左端点，存储每个数出现的位置，用 set 维护当前左端点右边每种数第一次出现的位置，然后模拟上述跳跃过程。跳跃次数与数字的种类有关，而每个段中剩余数字不会超过 $\sqrt{n}$ ，且根号并不会跑满，该做法可以接受。

时间复杂度为 $O\left(\frac{n^2}{x}\right)$ 。

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define endl '\n'
const int M = 1e6 + 5, N = 1e6 + 5;
int a[M], b[M];

void solve()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)
        cin >> a[i], b[i] = a[i] ;
    sort(b + 1, b + 1 + n);
    int cnt = unique(b + 1, b + 1 + n) - b - 1;
    for (int i = 1; i <= n; ++i)
        a[i] = lower_bound(b + 1, b + 1 + cnt, a[i]) - b;
    vector<int> c(cnt + 1);
    for (int i = 1; i <= n; ++i)
        c[a[i]]++;//每个数出现的次数
    int st = 1;
    vector<vector<int>> pos(n + 2);
    vector<int> gto(n + 2, 1e9);//第i个数需要往右跳跃所到的位置
    vector<int> ans(n + 2, -1);
    auto fun = [&](int x, int y) -> void//处理某个段
    {
        for (int i = x; i <= y; ++i)
            pos[a[i]].clear();
        set<int> p;
        for (int i = y; i >= x; --i)
        {
            if (pos[a[i]].size())
                p.erase(pos[a[i]].back());
            pos[a[i]].push_back(i);
            p.insert(i);
            if (pos[a[i]].size() >= m)
                gto[i] = pos[a[i]][pos[a[i]].size() - m];
            int r = i;
            // cout << "L=" << i << ":";
            // for (auto v : p)
            // {
            //     cout << v << ' ';
            // }
            // cout << endl;
            // cout<<i<<' '<<gto[i]<<endl;
            // cout<<i<<"  goto="<<gto[i]<<endl;
            for (auto v : p)
            {
                if (v <= r)
                    r = max(r, gto[v]);
                if (r == 1e9)
                {
                    r = -1;
                    break;
                }
            }
            ans[i] = r;
        }
    };
    for (int i = 1; i <= n; ++i)
    {
        if (c[a[i]] < m)//出现次数小于m的地方进行分段
        {
            int l = st, r = i - 1;
            if (l <= r)
                fun(l, r);
            st = i + 1;
        }
    }
    if (st <= n)
        fun(st, n);//最后一段单独处理
    for (int i = 1; i <= n; ++i)
        cout << ans[i] << ' ';
    cout << endl;
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;

    cin >> T;
    while (T--)
    {
        solve();
    }
}

F

先判断 $-1$ ， $m$ 个标记点，多源 bfs 求出每个点 $i$ 与 $m$ 个标记点的最短距离，记为 $f(i)$ 。

设 $dis(i,j)$ 表示结点 $i$ 与 $j$ 的距离。

对于每次询问：

当 $dis(x,y)＞f(y)$ 时显然不能获得冠军，输出 $-1$ 。
当 $dis(x,y)＜f(y)$ 时，说明小明是唯一冠军，直接输出 $0$ 。
下面就是 $dis(x,y)＝f(y)$ ：

也就是说从 $x$ 到 $y$ 的路径中，一定会存在一个点 $z$ ，使得 $x$ 与某个运动员(具体是哪个运动员不关心)第一次在 $z$ 相遇。

既然是第一次相遇，说明 $x$ 到 $z$ 之前的路径是 $x$ 一个人走过来的，那么前面路径上面的所有点 $i$ 都满足 $dis(x,i)\neq f(i)$ 。因为如果两者相等，说明两者必会在点 $i$ 相遇，与 $z$ 是第一次相遇的位置矛盾。

在 $z$ 相遇以后，后面小明就可以与那个运动员保持步调一致，路径上后面的所有点 $j$ 都满足 $dis(x,j)=f(j)$ 。

因此可以二分第一次的相遇点与起点 $x$ 的距离，设当前距离为 $mid$ ，倍增求出从 $x$ 到 $y$ 的这条路径上面走 $mid$ 步所到达的点，设为 $t$ ，判断 $dis(x,t)$ 与 $f(t)$ 是否相等即可。

总的时间复杂度为 $O(q \log^2 n)$

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int M = 2e5 + 5;
int fa[M][22], dep[M];
vector<int> f[M];
inline void dfs(int x, int t)
{
    fa[x][0] = t;
    dep[x] = dep[t] + 1;
    for (auto to : f[x])
        if (to != t)
            dfs(to, x);
}
inline int lca(int x, int y)
{
    if (dep[x] < dep[y])
        swap(x, y);
    for (int i = 20; i >= 0; i--)
    {
        if (dep[fa[x][i]] >= dep[y])
            x = fa[x][i];
    }
    if (x == y)
        return x;
    for (int i = 20; i >= 0; i--)
    {
        if (fa[x][i] != fa[y][i])
        {
            x = fa[x][i];
            y = fa[y][i];
        }
    }
    return fa[x][0];
}
int dis(int x, int y)
{
    return dep[x] + dep[y] - 2 * dep[lca(x, y)];
}

void solve()
{
    int n, m, q;
    cin >> n >> m >> q;
    for (int i = 1; i < n; ++i)
    {
        int x, y;
        cin >> x >> y;
        f[x].push_back(y);
        f[y].push_back(x);
    }
    dfs(1, 0);
    for (int j = 1; (1 << j) <= n; ++j)
        for (int i = 1; i <= n; ++i)
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
    vector<int> vis(n + 3, 1e9);
    queue<int> p;
    for (int i = 1; i <= m; ++i)
    {
        int x;
        cin >> x;
        vis[x] = 0;
        p.push(x);
    }
    while (!p.empty())//多源bfs预处理
    {
        int x = p.front();
        p.pop();
        for (auto to : f[x])
        {
            if (vis[to] > vis[x] + 1)
            {
                vis[to] = vis[x] + 1;
                p.push(to);
            }
        }
    }
    auto check = [&](int mid, int s, int t) -> bool//从s出发，往t走mid步，能否到达一个vis值为mid的点
    {
        int L = mid; // 距离
        int lc = lca(s, t);
        int d1 = min(dep[s] - dep[lc], mid);
        mid -= d1;
        for (int i = 0; i <= 20; i++)
        {
            if (1 << i & d1)
            {
                s = fa[s][i];
            }
        }
        if (mid)
        {
            int d2 = dep[t] - dep[lc] - mid;
            swap(s, t);
            for (int i = 0; i <= 20; i++)
            {
                if (1 << i & d2)
                {
                    s = fa[s][i];
                }
            }
        }
        return vis[s] == L;
    };
    while (q--)
    {
        int s, t;
        cin >> s >> t;
        int dist = dis(s, t);

        if (dist > vis[t])
            cout << -1 << endl;
        else
        {
            int ans = dist, l = 0, r = dist;
            while (l <= r)
            {
                int mid = l + r >> 1;
                if (check(mid, s, t))
                {
                    ans = mid;
                    r = mid - 1;
                }
                else
                    l = mid + 1;
            }
            cout << dist - ans << endl;
        }
    }
    for (int i = 1; i <= n; ++i)
    {
        f[i].clear();
        dep[i] = 0;
        for (int j = 0; j <= 20; ++j)
            fa[i][j] = 0;
    }
}
signed main()
{
    ios ::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)
        solve();

    return 0;
}

G

原问题转化一下，即：

把 $n$ 个数分为两组，每组的极差（最大值与最小值的差）不能超过 $k$ ，最小化 $k$ 。

问题等价于最小化两组极差的最大值。

设第一组的最小、最大值分别为 $x_1,y_1$ ，第二组的最小、最大值分别为 $x_2,y_2$ 。

这里假设 $y_1 \leq y_2$ ，于是 $x_1 \leq y_1 \leq y_2,x_2 \leq y_2$

结论：当取最优解时，必有 $y_1 \leq x_2$ ，即 $x_1 \leq y_1 \leq x_2 \leq y_2$ 。（两组之间一定不会有重叠部分）

证明：

设 $x_1,y_1,x_2,y_2$ 四个数经排序后从小到大为 $a,b,c,d,a\leq b \leq c \leq d$

当 $y_1 \leq x_2$ 时，此时两组极差的最大值为 $k_1=max(b-a,d-c)$
当 $y_1 > x_2$ 时，存在两类情况：
- 若 $x_1 \le x_2$ ，则排序为 $a=x_1,\ b=x_2,\ c=y_1,\ d=y_2$ 。此时两组极差的最大值为 $k_2=\max(c-a,\ d-b)$
- 若 $x_1 > x_2$ ，则排序为 $a=x_2,\ b=x_1,\ c=y_1,\ d=y_2$ 。此时两组极差的最大值为 $k_3=\max(c-b,\ d-a)=d-a$
这三类情况中，显然第三类是最大的（因为第二组覆盖的值域包含了第一组覆盖的值域，这种情况肯定不是我们想要的）。
因此只要讨论前两种情况，因为 $a\leq b \leq c \leq d$ ，所以 $b-a \le c-a ,d-c \le d-b$ ，即 $k_1=max(b-a,d-c) \leq k_2=\max(c-a,\ d-b)$
因此 $k_1 \leq k_2$ ，所以 $y_1 \leq x_2$ 时最优，即两组的值域部分不会有重叠。

因此只需要枚举 $y_1$ 所在位置， $y_1$ 以及它前面的数分到第一组， $y_1$ 后面的数分到第二组，对二者取最大值，再与答案取最小即可。

时间复杂度为 $O(n \log n)$ ，来自排序。

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int N = 1e6 + 5;
const int mod = 1e9 + 7;
int a[N];
void solve()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    int ans = 1e9;
    sort(a + 1, a + n + 1);
    for (int i = 1; i < n; i++)
        ans = min(ans, max(a[i] - a[1], a[n] - a[i + 1]));
    cout << ans << endl;
}
signed main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int T = 1;
    cin >> T;
    while (T--)
    {
        solve();
    }
}

H

签到，略

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
int w(string s)
{
    int n = s.size();
    int a = 0, b = 0, c = 0;
    for (int i = 0; i + 3 < n; ++i)
        if (s.substr(i, 4) == "fire")
            a++;
    for (int i = 0; i + 4 < n; ++i)
        if (s.substr(i, 5) == "water")
            b++;
    for (int i = 0; i + 3 < n; ++i)
        if (s.substr(i, 4) == "wind")
            c++;
    return a + b * c;
}
signed main()
{
    int T = 1;
    cin >> T;
    while (T--)
    {
        int x, y;
        cin >> x >> y;
        string a, b;
        cin >> a >> b;
        cout << (w(a) > w(b) ? "YES" : "NO") << '\n';
    }
    return 0;
}

I

直接根据向量偏移一下即可。


#include <bits/stdc++.h>
using namespace std;
#define int long long

signed main()
{
    int T = 1;
    cin >> T;
    while (T--)
    {
        int x1, y1, x2, y2, x3, y3;
        cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3;
        cout << (x1 + x2 - x3) << " " << (y1 + y2 - y3) << '\n';
    }
    return 0;
}

J

题目太长，略

K

两种解法。

方法一：参考 pdf 题解，我只提供代码。

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int M = 1e6 + 5;
int a[M], b[M];
void solve()
{
    int n, k;
    cin >> n >> k;
    vector<int> sum(n + 4), cnt(n + 4);
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        int t = 0;
        if (a[i] == k)
            t = 0;
        else if (a[i] > k)
            t = 1;
        else
            t = -1;
        cnt[i] = cnt[i - 1] + (t == 0 ? 1 : 0); // 统计前i个数中k的个数
        sum[i] = t + sum[i - 1];
    }
    vector<vector<int>> pos(2 * n + 4);
    pos[n].push_back(0);
    for (int i = 1; i <= n; i++)
        pos[sum[i] + n].push_back(i); // 由于sum可能为负数，所以整体平移n
    int res = 0;
    for (int i = 0; i <= 2 * n; ++i)
    {
        for (int j = 0, L = pos[i].size(); j < L; ++j) // L表示pos[i]的大小
        {
            int x = pos[i][j];
            int l = j, r = L - 1, ans = -1;
            while (l <= r)
            {
                int mid = l + r >> 1;
                if (cnt[pos[i][mid]] - cnt[x]) // 判段区间内是否有k，只有至少有一个k才符合要求
                {
                    ans = mid;
                    r = mid - 1;
                }
                else
                    l = mid + 1;
            }
            if (ans != -1) // 找到了才加
                res += pos[i].size() - ans;
        }
    }
    cout << res << endl;
}

signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int T;
    cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

方法二：

设： $b_i=\left\{ \begin{aligned} & -1,&& a_i < k \\ & 0, && a_i = k \\ & 1, && a_i > k \end{aligned} \right.$

于是原问题等价为：序列 $\{b_1,b_2,...\dots b_n\}$ 有多少个子区间 $[L,R]$ ，使得区间中至少存在一个 $0$ ，且区间和 $\sum_{i=L}^{R} b_i$ 的值为 $0$ 。

如果没有区间至少有一个 $0$ 的限制，这是一个经典的问题：预处理序列 $\{b_1,b_2,...\dots b_n\}$ 的前缀和，设为 $\{S_1,S_2,...\dots S_n\}$ 。对于一个给定的右端点 $R$ ，左端点 $L$ 满足条件当且仅当 $S_R-S_{L-1}=0$ 。

可以在顺序遍历枚举右端点的时候，维护每个 $S_i$ 出现的次数，对于当前枚举右端点的 $R$ ，让答案加上目前序列中 $S_R$ 出现的次数即可。

但是加上了每个区间至少有一个 $0$ 的限制呢？注意我们实际上只关心每个区间是否有 $0$ ，而不关心具体有多少个 $0$ ，因此对于当前枚举的右端点R，我们只需要知道上一个 $b_i$ 为 $0$ 的位置（也就是上一个 $a_i$ 为 $k$ 的位置），假设这个位置为 $x$ ，那么其实是在做这样的一次查询：

在 $x-1$ 的前面位置 $i(0\leq i \leq x-1)$ ，有多少 $i$ 满足 $S_i=S_R$ ？满足这个条件的 $i$ 加一之后其实就是我们要找的左端点。
设 $cnt(i,j)$ 表示 $\{S_0,S_1,S_2,...\dots S_i\}$ 中 $j$ 出现的次数，即查询 $cnt(x-1,S_R)$ 。

但是我们会枚举 $n$ 次右端点，难道我们需要开二维数组来维护 $cnt$ 吗？这样时间和空间复杂度都是 $O(n^2)$ 的，不可接受。

实际上，我们有 $n$ 次询问，每一次询问都可以表示成一个二元组 $x,y$ ，然后查询 $cnt(x,y)$ ，我们将所有的查询按 $x$ 升序排序之后，然后再遍历，并维护每个 $S_i$ 出现的次数，假如当前遍历到的位置为 $i$ ，我们需要把所有询问中（这 $n$ 次询问）满足 $x=i$ 的询问拿出来即可（可以用二维 vector 预处理实现），这样我们就不用 $O(n^2)$ 维护了（有点类似背包的滚动数组）。

实际处理也并不需要对所有询问的左端点排序，因为从小到大枚举就相当于给所有元素按左端点排好序了，这样最终的时间复杂度为 $O(n)$ 。

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int M = 1e6 + 5;
int a[M], b[M];
void solve()
{
    int n, k;
    cin >> n >> k;
    vector<int> sum(n * 2 + 4);
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        int t = 0;
        if (a[i] == k)
            t = 0;
        else if (a[i] > k)
            t = 1;
        else
            t = -1;
        sum[i] = t + sum[i - 1];
    }
    vector<vector<int>> query(n + 4);
    int pos = -1;
    for (int i = 1; i <= n; i++)
    {
        if (a[i] == k)
            pos = i;
        if (pos == -1)
            continue;
        query[pos - 1].push_back(sum[i]);//查询：sum数组中，pos-1的前面有多少个数等于sum_i
    }
    vector<int> cnt(2*n + 4);
    int ans = 0;
    for (int i = 0; i <= n; i++)
    {
        cnt[sum[i] + n]++;//由于sum可能是负数，我们在处理的时候给所有值往右偏移n个单位，这样得到的数字都为非负数了
        for (auto x : query[i])
            ans += cnt[x + n];
    }
    cout << ans << endl;
}

signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int T;
    cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

L

签到，略

cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long

signed main()
{
    int T = 1;
    cin >> T;
    while (T--)
    {
        int a, b;
        cin >> a >> b;
        cout << (a + b == 350234 ? "YES" : "NO") << '\n';
    }
    return 0;
}

M

这类模型似乎也是典中典了，我们先仅考虑 $h_1$ 和 $h_2$ 的关系，如果 $h_1>h_2$ ，那么我们无论如何都必须在第二个位置执行最少 $h_1-h_2$ 次，那么不妨直接对第二个位置进行 $h_1-h_2$ 次操作，这样带来的影响是：区间 $[2,x+1]$ 的数都被加了 $h_1-h_2$ 次，操作完后 $h_1,h_2$ 的大小关系已经满足条件了，然后依次往后做同样的操作即可。

显然，这里的区间操作我们可以用差分来维护，设 $d_i=h_i-h_{i-1}$ ，那么对区间 $[L,R]$ 的所有数字加上 $x$ 等价于 $d_{R+1}-=x,d_L+=x$ 。


#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int M = 1e6 + 5;
int a[M];
void solve()
{
    int n, x;
    cin >> n >> x;
    vector<int> d(2 * n + 2); // 差分数组
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        d[i] = a[i] - a[i - 1];
    }
    int ans = 0; // 总操作次数
    for (int i = 1; i <= n; i++)
    {
        if (d[i] < 0)
        {
            int cnt = abs(d[i]); // 操作次数
            ans += cnt;
            d[i] = 0;
            d[i + x] -= cnt; // 更新差分数组
        }
    }
    cout << ans << endl;
}
signed main()
{
    ios ::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)
        solve();

    return 0;
}

2025-11-28

先去官网下载源码，https://tools.icpc.global/

滚榜的部分只需要 resolver 就行了，记得下载稳定版。

如果你在使用该项目时出现错误，请务必和我一样的 resolver 和 domjudge 版本，我的 domjudge 使用的是 8.3.1，参考 http://blog.zymusic.top/post/36 里的docker-compose。

注意

此项目只针对 domjudge 使用，其他 oj 滚榜不可使用。

请在 domjudge 部署后将配置这里的 Data source 切换为 external，因为据说不切换会有很多锅？（因为数据库里面有自己的自增的整数主键 id 值，然而我们在导入用户信息的 id 却是手动设置的（而且一般都是字符串），如果我们想使用自己设置的 id，应该是对应 external id （我猜测的，如果 id 不对，那这个项目肯定就会出问题了）） ![image.png](https://blog.zymusic.top/static/img/993e7f5d3eb4eae994a0c9a5c8dd54cb.image.webp

下载

sh
git clone https://gitee.com/ai-ziming/icpc-award-tracker-tool.git
cd icpc-award-tracker-tool
sudo apt install npm -y
npm install

在 icpc-award-tracker-tool 目录下创建文件.env

由于数据来源是直接查询数据库的，所以需要配置 mysql 连接信息。


DB_HOST=192.168.88.134 # 数据库地址
DB_PORT=13306 # 数据库端口
DB_USER=root # 数据库用户
DB_PASSWORD=123456 # 数据库密码
DB_NAME=domjudge # 数据库名称
PORT=3000 # 应用程序端口

这里的配置一定要提前修改好，如果你不知道账号密码端口，请查看你部署 domjudge 时的配置信息文件。

注

注意：由于此项目会查询 domjudge 的数据库，请不要在比赛期间频繁使用这个项目，防止对比赛的数据库造成压力，应该等比赛结束之后再来访问，因为我们的目的只是设置奖项。

如果你的项目部署在公网服务器上，请开放对应的端口（这里的 13306 给你的源 ip，或者对所有源开放（不推荐）），如果你不开放，即使数据库配置信息正确也连接不上。

启动，生成奖项

然后就可以启动了

sh
npm run dev

访问 http://localhost:3000 。

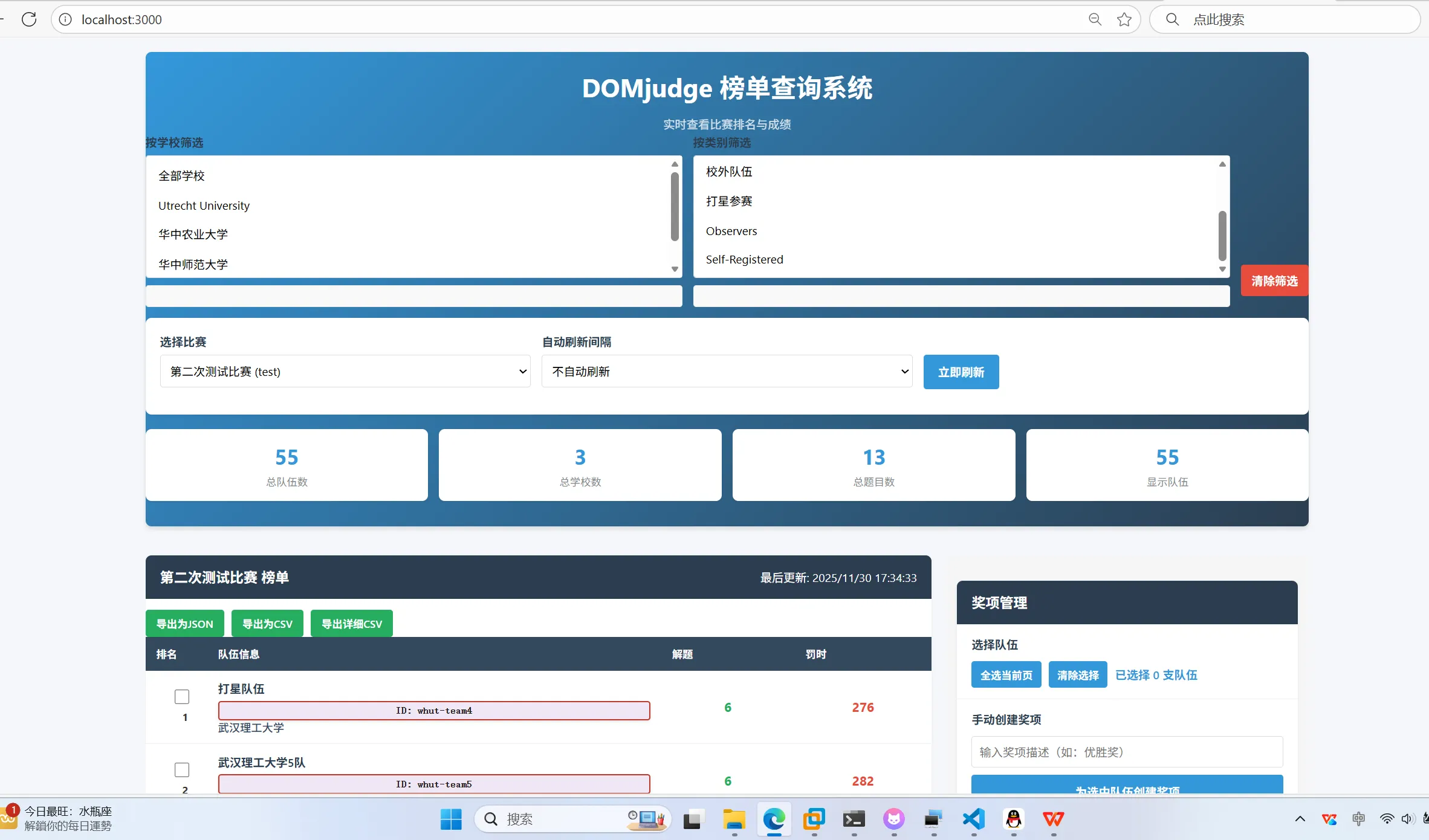
上面可以筛选指定的学校和分类

目前我筛选了华中农业大学的队伍，然后为华中农业大学所有队伍生成 1-3-5 的奖项，奖项的描述可以自己设定，注意逗号和冒号使用英文符号而不是中文符号。

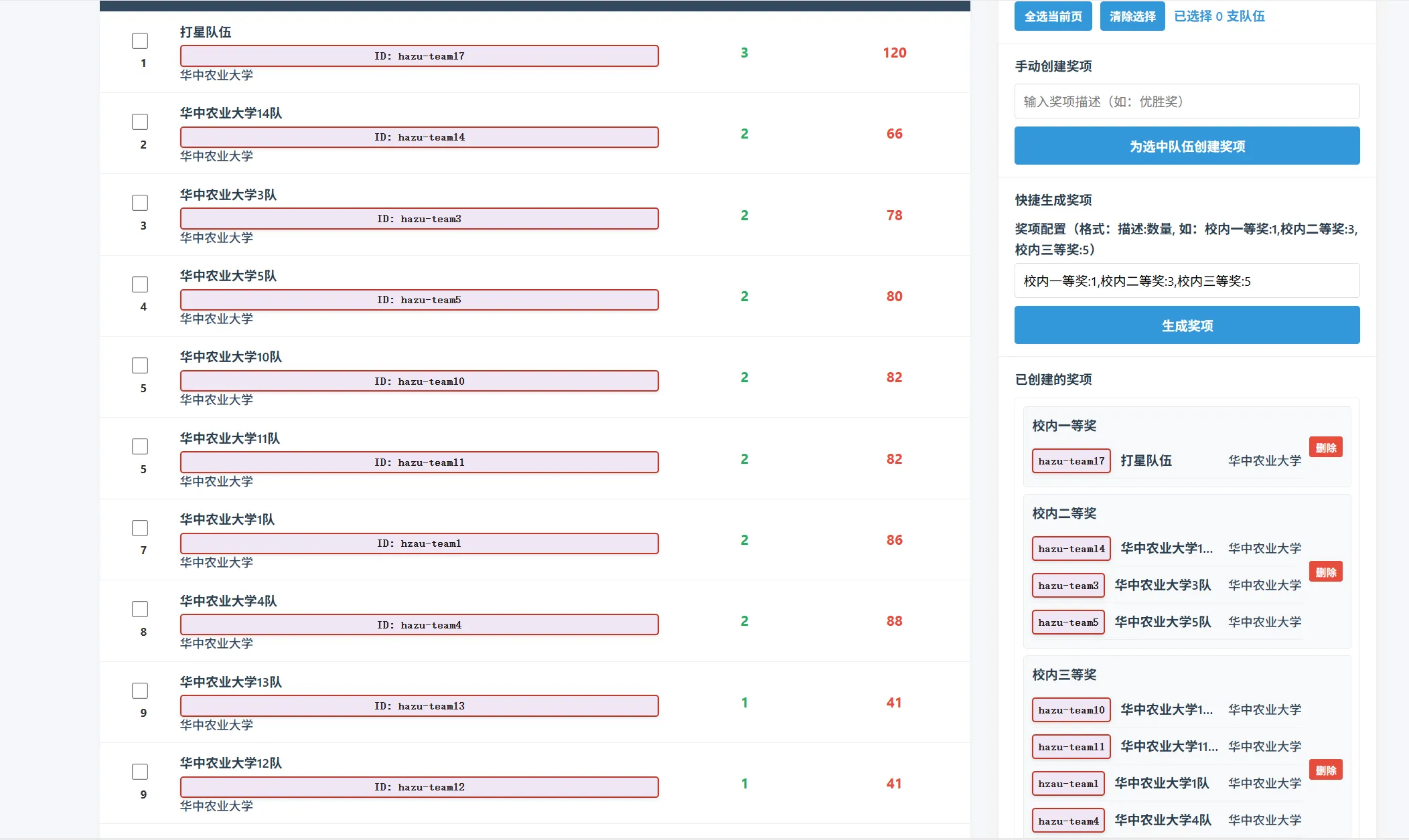
如果你想过滤掉打星队伍，在分类里面筛选一下即可。

同时，可以为所勾选的指定队伍列表设置自定义奖项。

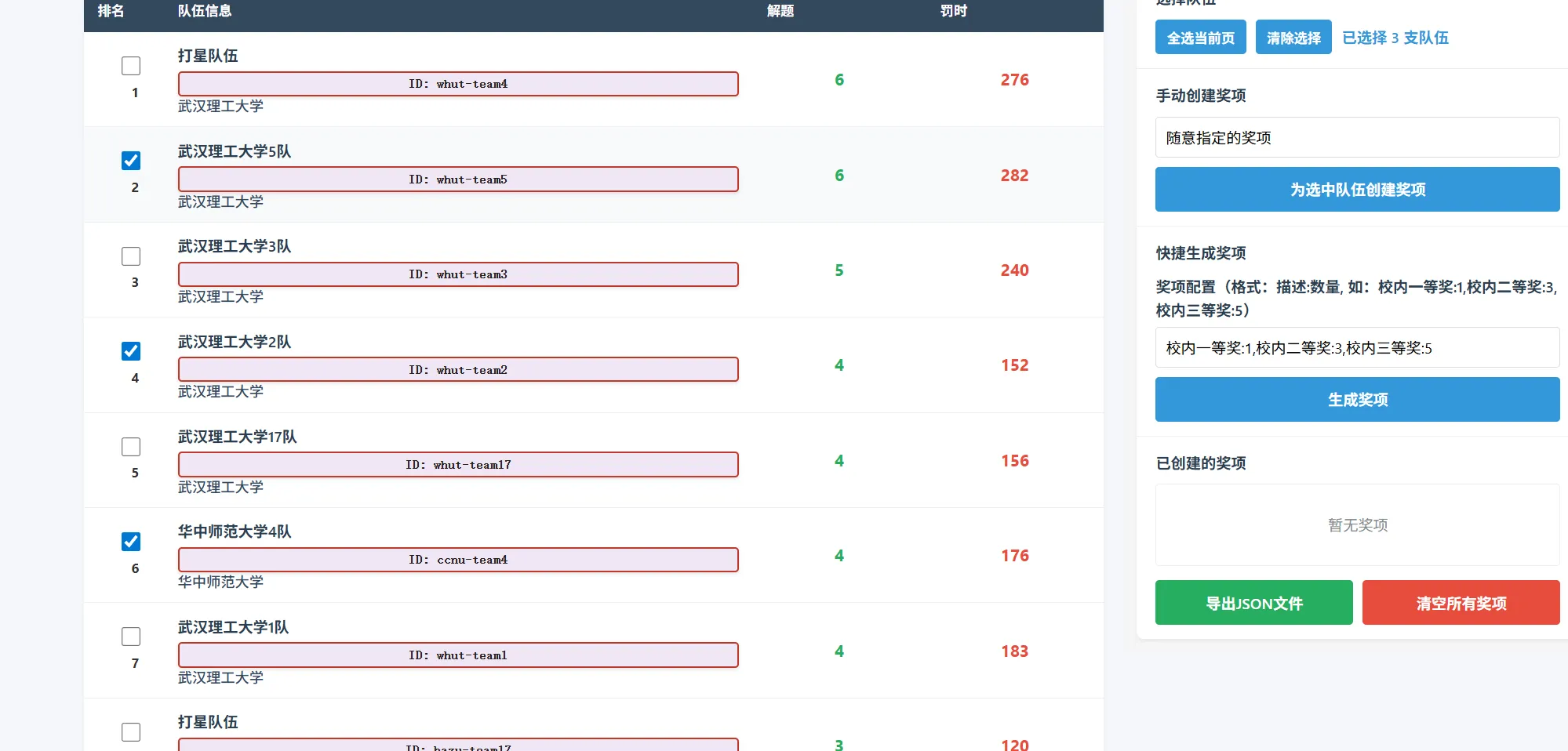
点击为选中队伍创建奖项，即可生成。

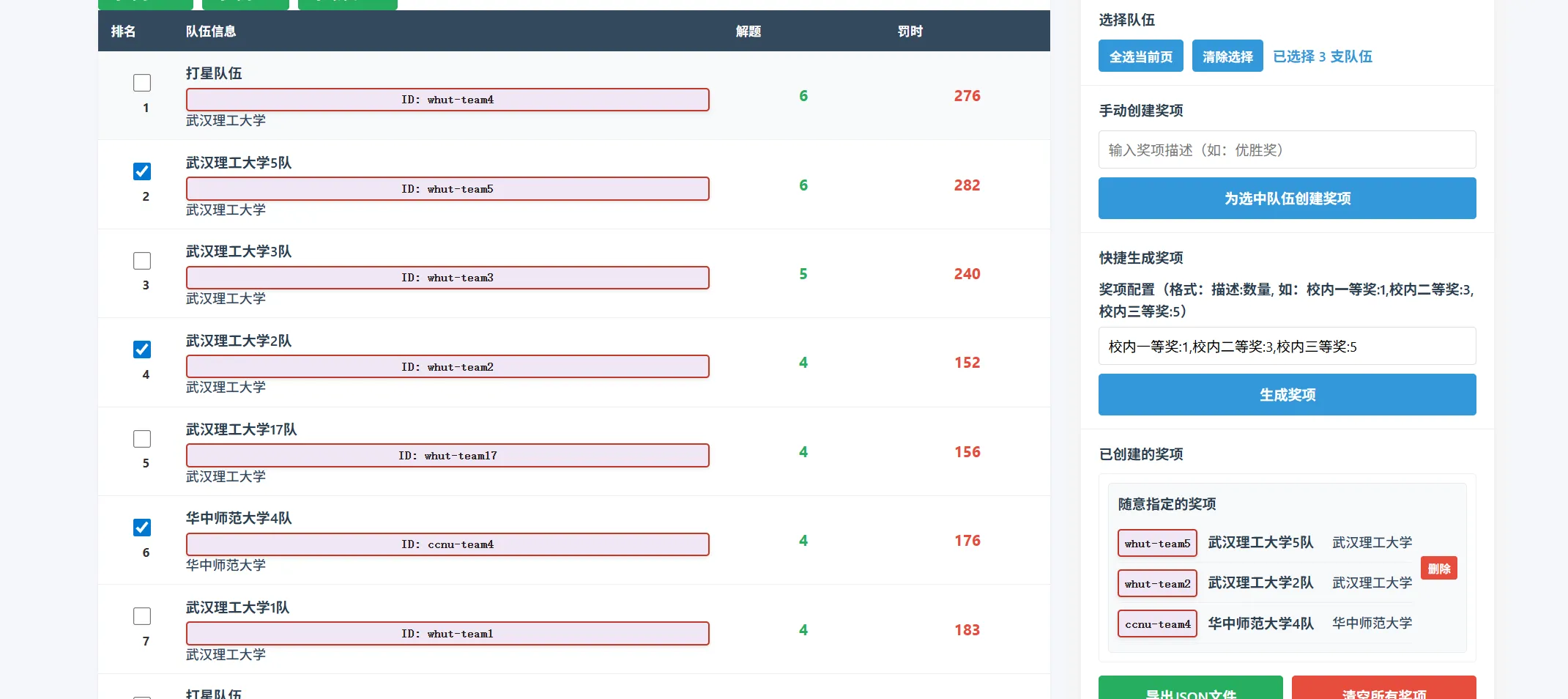
可以在这里预览所生成的所有奖项，防止出错。

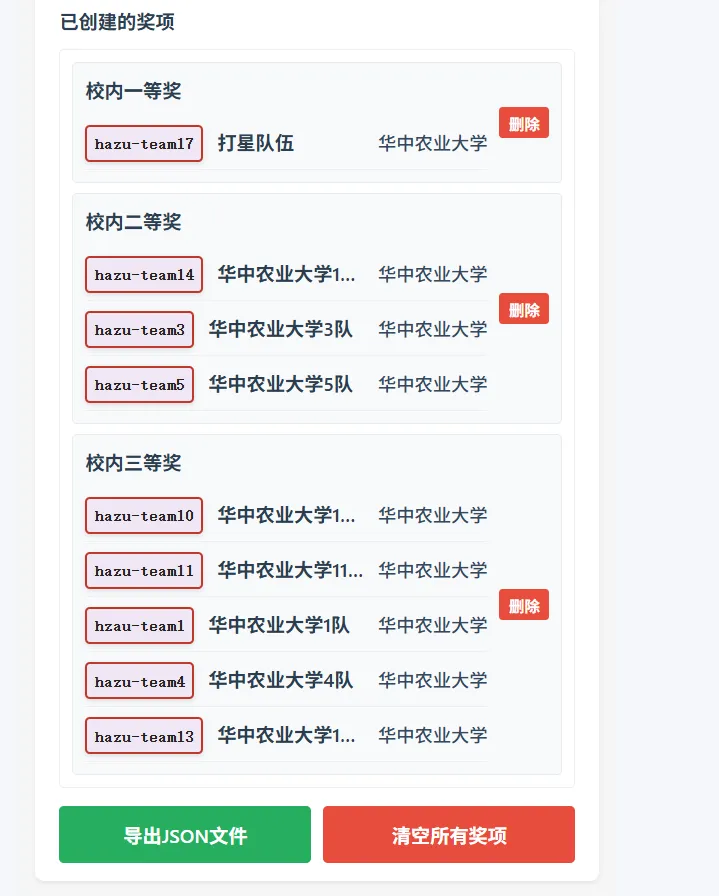
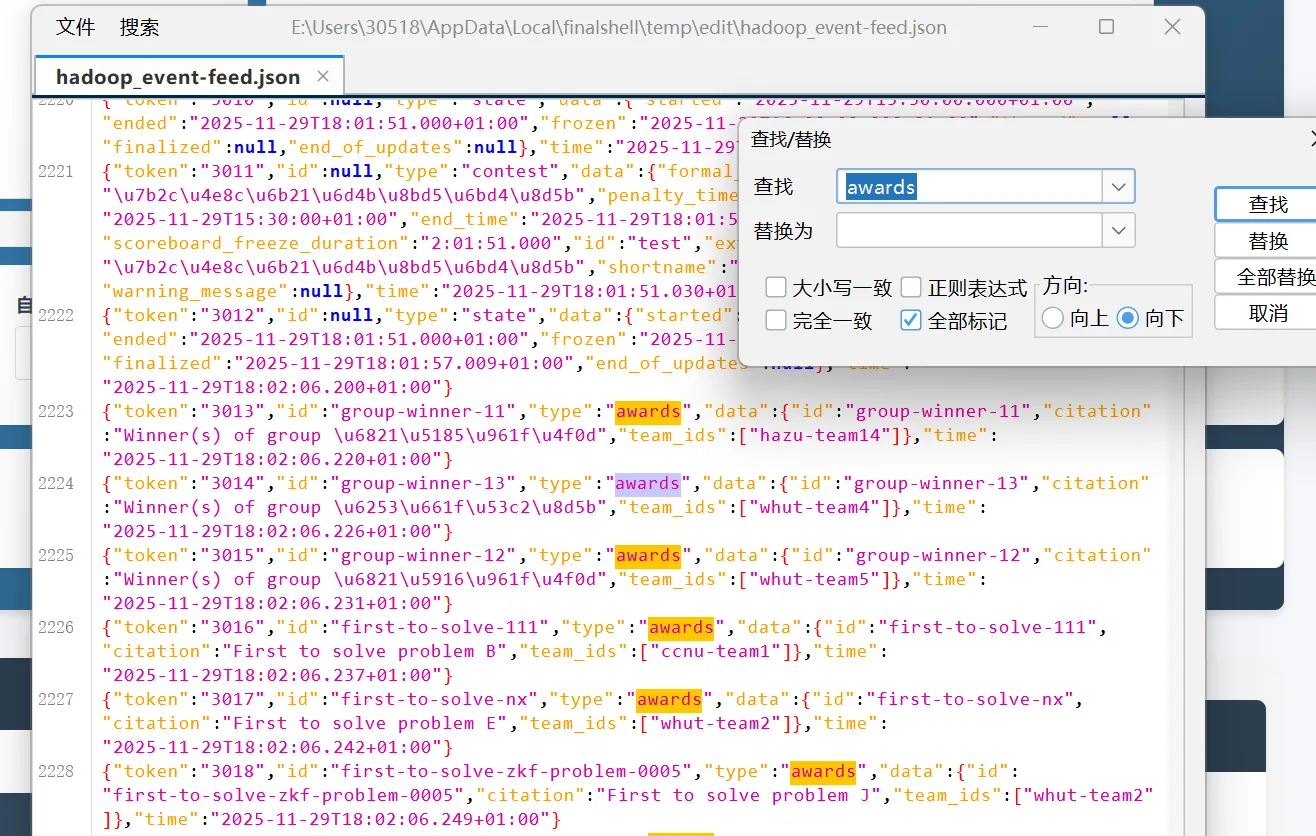
然后点击导出下载即可，得到的是 json 格式数据，请不要随意格式化或者修改数据格式，不要随意换行，因为 resolver 读取某个信息的时候是逐行读取的。

这里有用的信息其实就三个，type 为 awards，告诉 resolver 说这是一个奖项，id 是奖项的 id，从一个大数据开始不断往后面加 $1$ 即可，citation 是你自己设置的奖项描述

执行get-photo脚本，获取比赛数据和用户数据头像。

sh
chmod +x get-photo.sh
sudo apt install jq -y
./get-photo.sh 192.168.88.134 2bNx8Wn9OA5horS8_5-Wju test

这个脚本需要三个参数，第一个是 domjudge 的 ip 地址或者域名，第二个是 admin 用户的密码，第三个是比赛id。比赛 id 是这里的 external ID

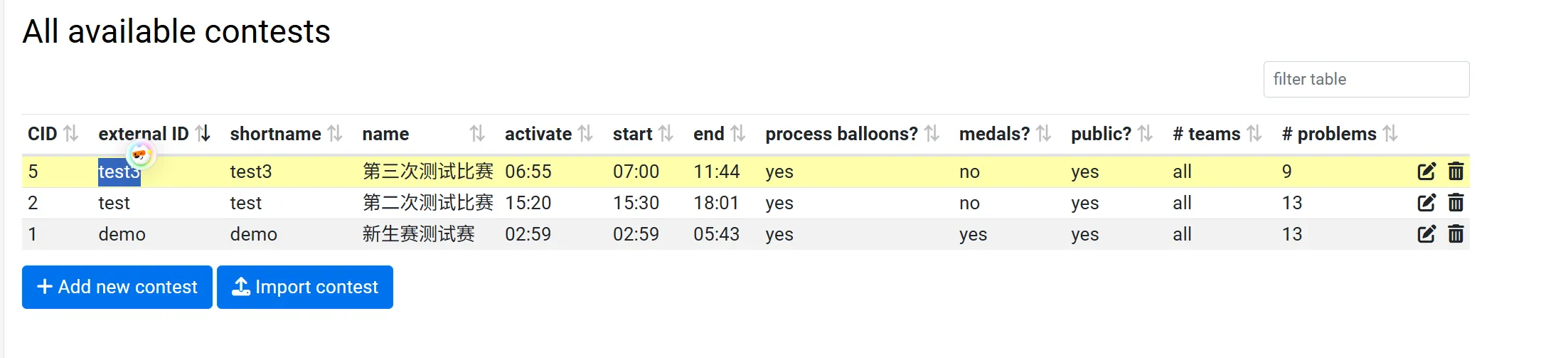
然后你就获得了比赛的信息，位于 my-contest 目录，包括队伍和学校的头像。

如果结果错误，下载不到数据，可能是 jq 版本不同导致的（我的版本是 1-6）

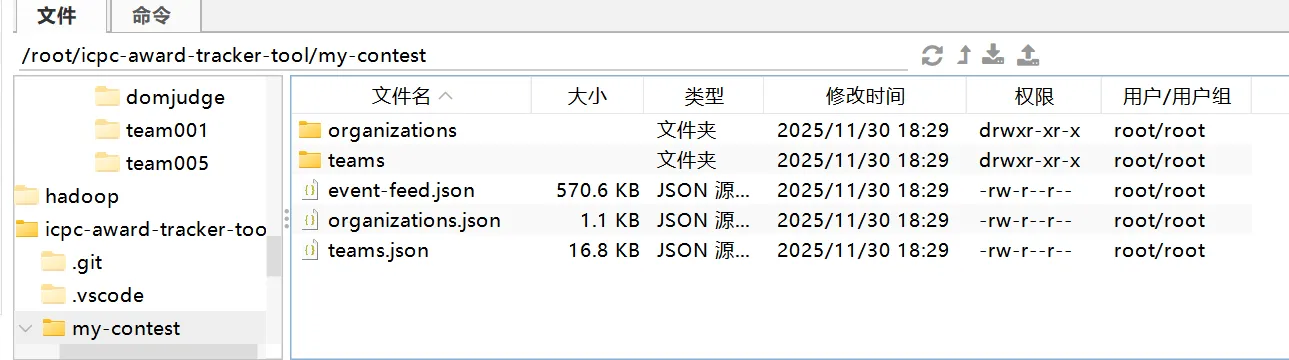
然后需要修改这里的 event-feed.json，把刚才导出奖项的 json 格式数据加到这个 event-feed 里面。

按 ctrl+f 搜索，删除一些不需要的奖项（因为 domjudge 会默认给我们生成一些奖项，比如一血，冠军之类的，他生成的默认奖项我们只保留一血奖就行，其他奖项统统删除，然后再把我们项目刚才生成的 json 数据直接复制到 event-feed 里面即可）

阅读全文